Using Heaps in Go (Golang)#

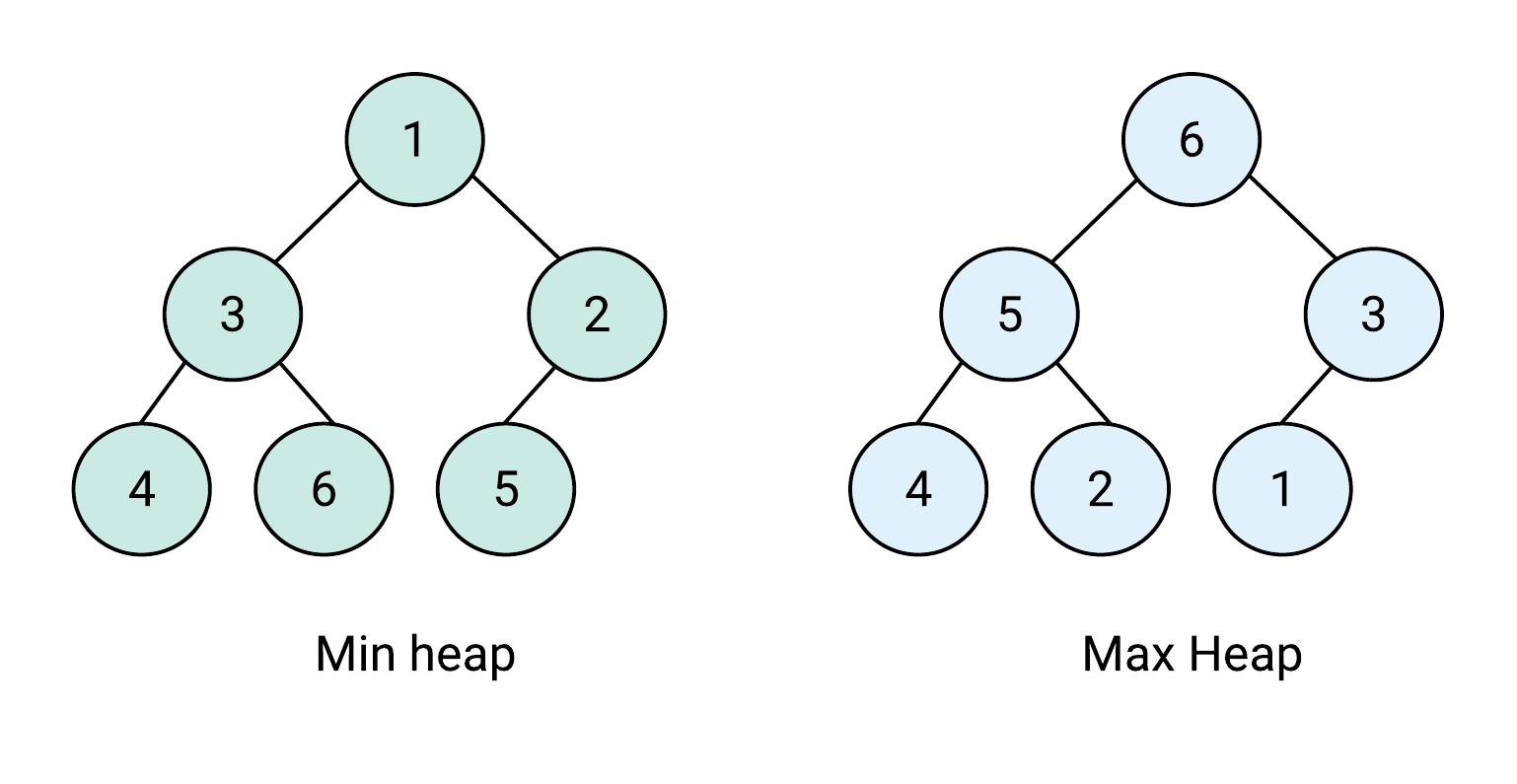Image Description Heaps (Priority Queues) are often used for implementing priority queues and efficient sorting algorithms. A heap is a special binary tree structure that satisfies the heap property:

Min-Heap: The value of each parent node is less than or equal to the values of its children.
Max-Heap: The value of each parent node is greater than or equal to the values of its children.

In this blog post, we will explore how to implement and use heaps in Go using the container/heap package.

Introduction to the `container/heap` Package#

Go’s standard library provides a heap package in the container module, which allows you to work with heaps. However, the heap package does not provide a built-in heap type like in some other languages (Python etc.). Instead, it allows you to define a custom type that implements the heap.Interface.

Key Functions in the `heap` Package#

heap.Init(h heap.Interface): Transforms the slice into a valid heap.
heap.Push(h heap.Interface, x interface{}): Adds an element to the heap.
heap.Pop(h heap.Interface) interface{}: Removes and returns the smallest (or largest, depending on the heap type) element from the heap.

To use the heap package, you must implement the following methods:

Len() int
Less(i, j int) bool
Swap(i, j int)
Push(x interface{})
Pop() interface{}

Implementing a Min-Heap in Go#

Let’s start by implementing a Min-Heap (where the smallest element is at the top of the heap). Here is an example:

package main

import (
	"container/heap"
	"fmt"
)

// Define a custom type for the heap
type IntHeap []int

// Implement the heap.Interface for IntHeap

// Len is the number of elements in the collection.
func (h IntHeap) Len() int { return len(h) }

// Less reports whether the element with index i should sort before the element with index j.
func (h IntHeap) Less(i, j int) bool {
	return h[i] < h[j] // Min-heap: smallest element should be at the top
}

// Swap swaps the elements with indexes i and j.
func (h IntHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

// Push adds an element to the heap.
func (h *IntHeap) Push(x interface{}) {
	*h = append(*h, x.(int))
}

// Pop removes and returns the smallest element from the heap.
func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

func main() {
	// Create an instance of the IntHeap
	h := &IntHeap{2, 1, 5}

	// Initialize the heap (heapify the slice)
	heap.Init(h)

	// Push an element onto the heap
	heap.Push(h, 3)

	// Pop elements from the heap
	fmt.Println("Min-Heap:")
	for h.Len() > 0 {
		// Pop and print the smallest element
		fmt.Printf("%d ", heap.Pop(h))
	}
}

Explanation:#

Custom Heap Type: We define IntHeap as a slice of integers ([]int) that will be used to implement our heap.
Implementing heap.Interface:
- Len(): Returns the number of elements in the heap.
- Less(i, j): Determines the ordering of elements; in this case, it’s set up for a Min-Heap where the smaller value should come first.
- Swap(i, j): Swaps two elements in the slice.
- Push(x): Adds a new element to the heap.
- Pop(): Removes and returns the smallest element from the heap.
Using the Heap:
- heap.Init(h) transforms the slice into a valid heap.
- heap.Push(h, 3) adds the value 3 to the heap.
- heap.Pop(h) removes and prints the smallest element from the heap, one by one.

Max-Heap Example#

To create a Max-Heap, where the largest element is at the top, we simply modify the Less() method to reverse the comparison:

// Less reports whether the element with index i should sort before the element with index j. 
func (h IntHeap) Less(i, j int) bool{ 	
	return h[i] > h[j] // Max-heap: largest element should be at the top 
}

With this change, the heap will behave as a Max-Heap.

When to Use Heaps?#

Heaps are especially useful for algorithms that need to efficiently retrieve the smallest or largest elements. Some use cases include:

Priority Queues: Heaps allow efficient insertion and extraction of elements based on priority.
Heap Sort: Heaps can be used to sort an array by repeatedly extracting the minimum (or maximum) element.
Dijkstra’s Algorithm: Heaps can be used for finding the shortest path in weighted graphs.

Advantages of Using Heaps#

Efficiency: Inserting and removing elements in a heap takes O(log n) time, which is faster than sorting the entire collection.
Memory Usage: Since heaps are implemented using arrays or slices, they provide a memory-efficient way to manage ordered data.

Conclusion#

In this post, we covered how to implement and use heaps in Go using the container/heap package. We demonstrated how to create both a Min-Heap and a Max-Heap and showed how you can use the heap to efficiently manage ordered data. Heaps are powerful tools for many algorithms, including priority queues and sorting, and they are a fundamental part of computer science.

Using Heaps in Golang